I think linear algebra is much wonderful magic and lore, and I think it's a lifelong commitment. As such, I've taken linear algebra refreshers and courses many, many times.
While I haven't found the holy grail of linear algebra courses yet - the course that unlocks linear algebra as a visual and geometric intuition, that is what I seek - I have found some good ones and some OK ones. And I figured I could review them all today! Why not!
MATH-310: Linear Algebra, American University
My first experience of linear algebra. I mean, I took this ~15 years ago (mamma mia). I remember enjoying it. I remember finding it deceptively simple. "Oh, it's all just basic math, only on series of numbers. How very plain!" Little did I know.
| Pros | Cons |
|---|---|
| Very positive experience! | Well, it was a long time ago. |
| Lots of fun! | Did I really dig into the theory of this stuff? |
| (False) sense of VERY EASY! |
Summer math camp, University of Oxford - MPhil in Economics program
Whence young folk go into econ grad school, thence are they usually exposed to a crash course of linear algebra (again, for many of them). I don't remember learning much here (sorry, Oxford! or maybe you should be apologizing to me, yeesh).
| Pros | Cons |
|---|---|
| Well, it was short. | Too short. |
| And a long time ago. |
Linear Algebra - Foundations to Frontiers (LAFF), UT-Austin, via EdX
This linear algebra course, offered freely via the EdX platform, is very highly rated and I was excited to take it. It also promised a visual-first teaching style, a "different" way of teaching linalg, and a very engaged set of professors and instructors.
Unfortunately, me and this course! We just didn't connect! I churned my way through about 1/3 of it before giving up.
| Pros | Cons |
|---|---|
| Proof-heavy. | Proof-heavy. |
| Free! | Forced use of their idiosyncratic/esoteric linear algebra software (instead of just numpy or something!) |
| Self-paced | Mostly theoretical. Most exercises/homework are proofs. |
| Always (?) available |
Linear algebra, Khan Academy
Honestly, Khan Academy has consistently blown my mind on such diverse topics as:
- Natural selection (MY MIND WAS BLOWN)
- Information theory (SO BLOWN)
- Renaissance Italian art (OMG AND I THOUGHT I KNEW ALL ABOUT THIS)
A lot of this has to do with Sal Khan's incredible clarity of thought, inherent pedagogical optimism/growth mindset, and his special talent of breaking everything down into a simple, understandable building block - and then using those blocks to build, ahem, TRULY INCREDIBLE TOWERS OF THOUGHT.
I love love love Khan Academy, it's one of my monthly charitable donations, and I recommend it to everyone for everything.
Anyway, so the linear algebra track! I switched to this from LAFF (above) and have slowly cobbled my way through it over the past N years (yes, years). Like LAFF, it is relatively heavy on proofs. Unlike LAFF, it starts with getting some of the basics of linear algebra calculations out of the way - there are a good number of exercises in the early sections which help you get some sense of doing basic calculations with vectors and matrices.
That said - it quickly takes off and becomes a lecture series of Sal Khan working through various proofs. This has pros and cons: a main pro is that Sal Khan is one of the few people I've found that can walk you through a proof in a way that feels instantly clear and simple. He's just good at it. And I've had many "ah ha" moments. The main con is sticking power: after Sal walks me through a proof, I'm like "ah ha, okay... now what?" There's no immediate application. There's rarely even a real world example of how/why this is amazing or useful. And thus I find it basically impossible to retain the takeaway.
Whereas that's what I want! I want to develop an intuitive understanding of linear algebra such that I can "see" the changes visually. See my post on Jacobian transformations for an example of when it has "clicked".
| Pros | Cons |
|---|---|
| Proof-heavy. | (Eventually) proof-heavy. |
| Free! | Exercises dwindle after an initial burst - there aren't many other ways to stay engaged. |
| Self-paced | Limited real-world examples/applications to work through or think about. |
| Always available | |
| Sal Khan is a great teacher. Maybe the best! | |
| More use of visual/geometric examples. |
Linear algebra refresher, Udacity and Georgia Tech
This one is freshest in my mind (since I've been working through it over the last couple days), and it's also my first semi-official introduction to the OMSCS. I was a little irritated with this course, though, since the idea was great but the execution was uggghhh.
The idea was: let's refresh/learn the basic ideas of linear algebra by building our own linear algebra library! In any language we like! Sounds great.
The execution though, was really, really painful. The instructor would quickly go over some major, deep linear algebra concept - such as determining whether two lines are parallel - and then would introduce the exercise. All the exercises have taken the same form: you are given - via a screenshot (!) of long, arbitrary floats (!!) - some example vectors, and you have to manually peck these long, arbitrary floats into your program (mine was also in Python, like the instructor's) to then solve for whatever. This was only after the instructor mind-numbingly read out all of these numbers both before and after you submitted your responses.
Screenshot:
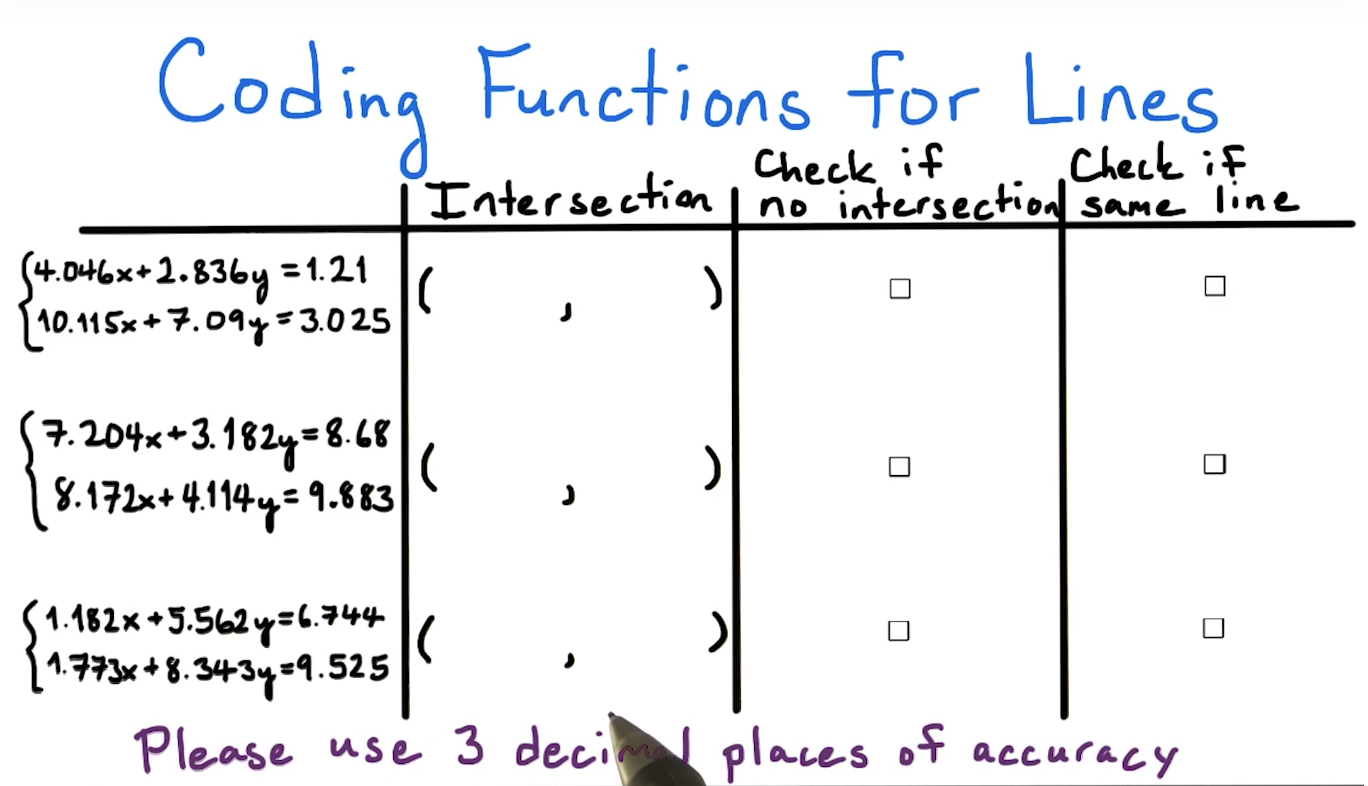
What in the Lord. What in the Lord?! Who thought this was a good idea? I spent like 40% of this refresher course manually pecking numbers and then, oh, making obvious human errors because manually transcribing numbers is an incredible waste of my time. Why didn't they just print the numbers as text?! Then I could copy-paste? Also, why did the instructor need to literally read out "four point zero four six ex plus two point eight three six why equals one point two one" both before and after, when he reads out the answers?! What an incredible waste of time and awful UX/UI. For shame!
For this reason, I'm only about halfway through this, and I'll choke the rest down (it's meant to only take a few hours, and I've been doing it here and there when I have a minute), but I'm really doubtful that I'll have any "ah ha" moments.
| Pros | Cons |
|---|---|
| Choose-your-language build-to-learn pedagogy. | SEVEN POINT TWO ZERO FOUR EX PLUS THREE POINT ONE EIGHT TWO WHY EQUALS PLEASE USE THREE DECIMAL PLACES OF ACCURACY WHY IN THE WORLD ARE WE PROVIDING EXERCISES BY MANUAL READ-OUT AND HANDWRITTEN SCREENSHOT |